Dies ist der vierte Teil der Serie Von den Zinsen leben – Entnahmestrategien unter der Lupe.
Hier geht’s lang zum ersten Teil und zur Übersicht.
Im letzten Artikel der Serie haben wir zwei große Klassiker der Rentenplanung genauer kennengelernt. Die Studie von William Bengen, die erstmals das Sequence-of-Returns-Risiko bei der Entnahme berücksichtigte und damit die berühmte 4 %-Regel prägte. Und die Trinity Study, die Bengens Arbeit um das Konzept der Erfolgswahrscheinlichkeit erweiterte.
Beide Studien nutzten dabei ein ganz ähnliches Verfahren. Sie nahmen eine (möglichst lange) Zeitreihe historischer Aktienrenditen und ließen ein fiktives Wertpapier-Portfolio verschiedene Zeiträume aus dieser Reihe durchlaufen. Am Ende jedes Zeitraums prüften sie: Hätte das Portfolio den Zeitraum überstanden? Bei der Trinity Study bildete der Anteil der erfolgreich verlaufenen Zeiträume dann die Erfolgswahrscheinlichkeit des getesteten Portfolios.
Doch bei dieser Art von Tests mit historischen Daten gibt es auch einige Unzulänglichkeiten.
Problem 1: Aufzeichnungen historischer Renditen sind nicht so leicht zu bekommen
Erst in den vergangenen Jahrzehnten wurden Kursdaten aus der ganzen Welt detailliert erhoben und öffentlich zugänglich gemacht. So richtig langfristige und vollständige Aufzeichnungen gibt es quasi nur aus den USA, die den größten und ältesten modernen Wertpapiermarkt besitzen.
Wade Pfau nutzt für seine Untersuchungen beispielsweise drei Datenquellen.1
Zum einen Ibbotson’s Stocks, Bonds, Bills and Inflation Yearbook, das wir schon von William Bengen und der Trinity Study kennen.
Dann die umfangreiche Datensammlung von Wirtschafts-Nobelpreisträger Robert Shiller, Erfinder des bekannten Shiller-KGV. Dessen Daten sind im Internet frei zugänglich und umfassen den US-Aktien- und Anleihenmarkt seit 1871.
Für den globalen Aktienmarkt nutzt Pfau schließlich das Dimson-Marsh-Staunton Global Returns Dataset. Das enthält jährliche Renditen für 20 große Industrieländer seit dem Jahr 1900. Ähnlich wie das SBBI Yearbook sind auch die DMS-Daten nur gegen Bezahlung zu bekommen.
Man sieht bereits: Sobald man die USA verlässt, werden die Daten deutlich knapper und weniger umfangreich.
Problem 2: Historische Renditen zeigen nur die Vergangenheit (und sind parteiisch)
Historische Daten decken zwar einen langen Zeitraum ab, kennen aber leider nicht die Zukunft. In den kommenden Jahrzehnten können aber auch ganz andere Rendite-Reihenfolgen auftreten als wir sie aus der Vergangenheit kennen.
Dazu kommt noch ein anderes Phänomen. Bei Tests mit historischen Zeitreihen ist der mittlere Teil der genutzten Datenreihe gegenüber den „Rändern“ oft übergewichtet. Testet man beispielsweise ein Portfolio mit allen überlappenden 30-Jahres-Zeiträumen zwischen 1900 und 2000, so ist das Jahr 1900 in nur einem einzigen Test-Zeitraum enthalten – dem von 1900 bis 1929. Jedes der Jahre zwischen 1930 und 1971 ist hingegen in dreißig Test-Zeiträumen enthalten. Dadurch sind die mittleren Jahre der Zeitreihe gegenüber denen am Anfang und am Ende überrepräsentiert.
Problem 3: Historische Daten beachten nicht das aktuelle Marktumfeld
Im Augenblick sind die Aktienmärkte relativ hoch bewertet (im Vergleich zum historischen Durchschnitt). Außerdem befinden sich die Zinsen für Anleihen und Tagesgeld auf historischem Tiefstand. Darum wäre es zurzeit risikoreicher, sich mit einem Wertpapier-Portfolio zur Ruhe zu setzen als im historischen Mittel.
Rechnet man mit historischen Datenreihen bekommt man als Ergebnis aber immer nur den historischen Durchschnitt, ohne Rücksicht auf möglicherweise besondere Marktsituationen.
Versteht mich nicht falsch: Für viele Modelle und Berechnungen sind historische Daten super geeignet und völlig ausreichend. Möchte man aber ein größeres Spektrum möglicher Rendite-Reihenfolgen testen oder Sondersituationen untersuchen, kommt man mit historischen Renditen nicht weiter.
Wie kann man diese Einschränkung umgehen? Dazu müsste man künstliche Rendite-Reihenfolgen erzeugen, die zwar keine echten historischen Zeiträume repräsentieren, aber vergleichbare Eigenschaften aufweisen (z.B. eine ähnliche Durchschnitts-Rendite und/oder Volatilität).
Genau das leisten Monte-Carlo-Simulationen.
Der Rendite-Würfel: Monte-Carlo-Simulationen
Monte-Carlo-Simulationen stammen eigentlich aus der angewandten Mathematik (genauer gesagt: der Wahrscheinlichkeitslehre oder Stochastik). Dabei handelt es sich um ein Verfahren, bei dem man ein Zufallsexperiment sehr viele Male wiederholt, um die Wahrscheinlichkeit eines bestimmten Ereignisses zu bestimmen.
Ein einfaches Monte-Carlo-Experiment könnte zum Beispiel darin bestehen, ein paar Tausend Mal einen Würfel zu werfen und dabei mitzuzählen, wie oft welche Zahl gewürfelt wird. Auf diese Weise könnte man feststellen, ob zum Beispiel die Sechs bei deutlich mehr als einem Sechstel der Würfe fällt – der Würfel also gezinkt ist.
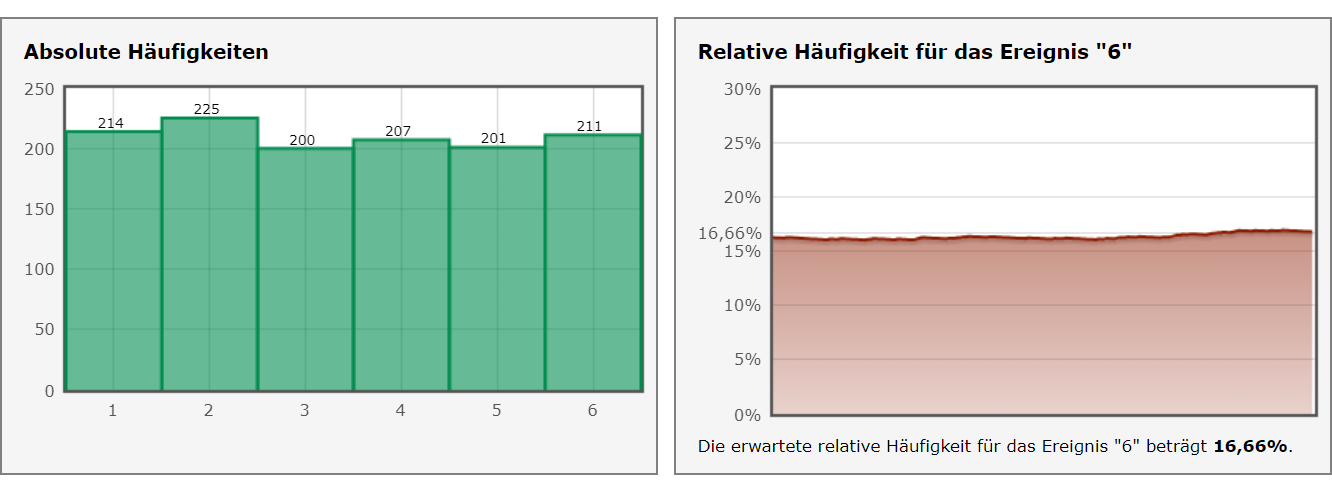Häufigkeitsverteilung beim Würfeln nach ca. 1.200 Würfen.
(Quelle: Würfel-Simulator der TU Clausthal, https://www.mathematik.tu-clausthal.de/interaktiv/simulation/wuerfel/)
Bei Monte-Carlo-Simulationen benötigt man im Regelfall sehr viele Wiederholungen (meistens einige 1.000 bis 100.000), damit man ein aussagekräftiges, statistisch signifikantes Ergebnis erhält. Darum kam diese Art von Experimenten etwa zeitgleich mit den ersten Computern auf, mit denen so viele Wiederholungen in der Praxis erst möglich geworden sind.
Der Name leitet sich übrigens tatsächlich vom gleichnamigen Casino-Stadtteil in Monaco ab. Der amerikanische Computerpionier John von Neumann wählte diese Bezeichnung, weil Wahrscheinlichkeiten auch an den Roulette-Tischen in Monte Carlo eine große Rolle spielen.
Wie helfen uns Monte-Carlo-Simulationen bei der Rentenplanung?
Mit dem Würfel-Experiment können wir herausfinden, wie hoch die Wahrscheinlichkeit ist, bei einem Würfel eine Sechs zu würfeln. Und auf ganz ähnliche Weise können wir mit einer Monte-Carlo-Simulation auch die Erfolgswahrscheinlichkeit eines Portfolios ermitteln. Dafür müssen wir natürlich keine Zahlen würfeln, sondern Test-Zeiträume mit zufälligen Rendite-Reihenfolgen erzeugen. Wenn wir beispielsweise Zeiträume mit einer Länge von 30 Jahren testen wollen, „würfeln“ wir dafür mehrere Tausend Mal jeweils 30 zufällige Jahresrenditen. Anschließend lassen wir – genau wie beim Test mit historischen Daten – unser Portfolio alle diese Testzeiträume durchlaufen.
Natürlich sollen die „gewürfelten“ Renditen nicht völlig zufällig sein. Die Test-Zeiträume, die dabei herauskommen, sollen ja möglichst ähnliche Eigenschaften besitzen wie der echte Aktienmarkt. Um das zu gewährleisten, gibt es bei Monte-Carlo-Simulationen prinzipiell zwei Möglichkeiten.
Variante 1: Zufällige Rendite-Reihenfolgen aus historischen Renditen erzeugen
Das wäre in etwa so, als würden wir die historischen Renditen auf einen großen Würfel schreiben (einen mit 100 oder mehr Seiten). Auf jede Seite des Würfels kommt dabei der Rendite-Wert eines „echten“ Jahres. Testet man einen 30-Jahres-Zeitraum, würfelt man 30 Mal hintereinander und erhält so eine neue zufällige Rendite-Reihenfolge.
Variante 2: Eine statistische Verteilung nutzen.
Alternativ kann man mit dem Computer auch völlig neue, zufällige Renditewerte erzeugen. Dabei kann man festlegen, dass diese einer bestimmten statistischen Verteilung folgen sollen.
Ein relativ einfaches mathematisches Modell für Aktienrenditen ist zum Beispiel das von Black und Scholes. Demnach folgen Aktienrenditen ungefähr einer Normalverteilung. Diese Normalverteilung ist immer durch zwei Variablen definiert: Einem Erwartungswert und einer Standardabweichung. Der Erwartungswert ist in unserem Fall die Durchschnittsrendite unseres Aktienportfolios und die Standardabweichung entspricht der Volatilität der Rendite.
Nutzt man nun bei einer Monte-Carlo-Simulation eine Normalverteilung mit der gleichen Durchschnittsrendite und Volatilität des echten Aktienmarkts, so spuckt der Computer Zufallsrenditen aus, die den echten Aktienrenditen schon relativ ähnlich sind.2
Mit ein paar mathematischen Tricks kann man so ein Modell dann noch erweitern. Um etwa längere Bullen- oder Bärenmärkte zu simulieren, kann man beispielsweise eine serielle Korrelation zwischen den einzelnen Jahresrenditen herstellen (dafür nutzt man ein Verfahren namens Cholesky-Faktorisierung). Das bedeutet, dass die Renditen eines Jahres nicht komplett zufällig sind, sondern auch von den Renditen der vorherigen Jahre abhängen.
Wade Pfau nutzt diese Technik zum Beispiel in einer Monte-Carlo-Simulation, in der er die aktuell hohe Bewertung des Aktienmarkts und die niedrigen Zinsen stärker berücksichtigt. Dazu startet seine Simulation mit tendenziell niedrigeren Renditen, wie sie für die kommenden Jahren wahrscheinlicher sind. Mit der Zeit steigen diese Durchschnittswerte dann langsam wieder auf ihr historisches Mittel.
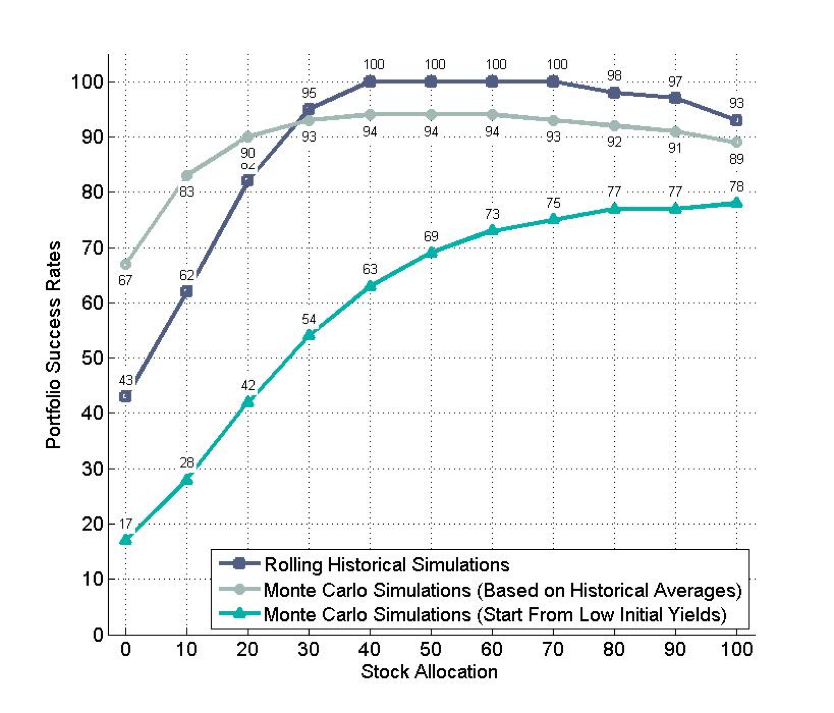
Die folgende Grafik zeigt das Ergebnis dieser Untersuchung. Sie stellt die Erfolgswahrscheinlichkeit des Portfolios in Abhängigkeit vom Aktienanteil dar – bei einer konstanten, inflationsbereinigten Entnahme von 4 % und einem Zeithorizont von 30 Jahren.
Die hellgrüne Linie unten ist das Ergebnis der Simulation unter Berücksichtigung der niedrigeren Renditen. Die dunkelblaue Linie stammt von einer historischen Simulation, die hellgraue Linie von einer Monte-Carlo-Simulation ohne Berücksichtigung des aktuellen Marktumfelds.
Portfolio-Erfolgswahrscheinlichkeiten für eine 4 % Entnahmerate. Rollierende historische Renditen vs. Monte-Carlo-Simulationen. Für eine Rente von 30 Jahren, inflationsbereinigt.
Aus: Pfau, Wade:Does The 4% Rule Work In Today’s Markets?. McLean Asset Management.
(Quelle: https://retirementresearcher.com/4-rule-work-todays-markets/)
Man erkennt, dass die aktuell sehr niedrigen Anleihenrenditen und die hohen Aktienmarktbewertungen die Erfolgswahrscheinlichkeit für Portfolios deutlich reduzieren, die gerade mit dem Entsparen beginnen. Wer heute in Rente geht, muss für die gleichen Erfolgschancen also über etwas mehr Vermögen verfügen, als die historischen Durchschnittswerte nahelegen.
Doch auch Monte-Carlo-Simulationen sind nicht perfekt und letztlich immer nur so gut wie ihre Eingabe-Parameter.
In vielen Untersuchungen liefern historische Daten und Monte-Carlo-Simulationen recht ähnliche Ergebnisse (wie Wade Pfaus Simulation oben). Doch je nach Experiment kommt es manchmal auch zu krassen Abweichungen. So hat Karsten Jeske, Autor des englischsprachigen FIRE-Blogs Early Early Retirement Now, eine Monte-Carlo-Studie von Wade Pfau und Michael Kitces einmal mit historischen Daten wiederholt – und kam zu deutlich anderen Ergebnissen als die beiden Wissenschaftler. Im Detail zeigt der echte Aktienmarkt dann eben doch so manches Verhalten, dass sich in Monte-Carlo-Simulationen nicht so einfach nachbilden lässt (zum Beispiel Mean Reversion oder behavioristische Effekte).
Nun aber genug der höheren Mathematik und zurück zu den Entnahme-Simulationen.
Deine eigene Trinity-Studie für Zuhause
Vor 20 Jahren lieferten Bengens Untersuchung und die Trinity-Study bahnbrechende Erkenntnisse für die Rentenplanung.
Heute aber leben wir im Jahr 2018 und die Zeiten haben sich geändert. Mittlerweile beschäftigt sich die Wissenschaft mit Cholesky-Faktorisierung, Log-TLF-Verteilungen und dynamischen Entnahmemodellen. So eine mickrige Trinity Study ist mittlerweile Standardkost, die heute jedermann mit ein paar Mausklicks von Zuhause durchführen kann – mit den passenden Tools.
Dafür habe ich heute zwei Videos mitgebracht, in denen ich euch zwei dieser Rechner einmal genauer vorstelle: den Vanguard Nestegg Calculator und den cFIREsim.
Mit diesen könnt ihr eure eigene kleine Entnahme-Simulation durchführen und dabei eure Wunsch-Parameter einstellen.
Beide Rechner sind im Internet frei verfügbar und laufen ganz einfach im Webbrowser.
Vanguard Nestegg Calculator
Der Vanguard Calculator ist einfach zu bedienen, bietet dafür aber auch nur wenige Einstellmöglichkeiten. Unter der Haube nutzt er Monte-Carlo-Simulationen auf Basis historischer Renditen.
Am besten gefällt mir an diesem Tool, dass man auf einen Blick erkennen kann, wie die Erfolgswahrscheinlichkeit mit steigendem Zeithorizont kontinuierlich abnimmt.
Mit dem Laden des Videos akzeptieren Sie die Datenschutzerklärung von YouTube.
Mehr erfahren
cFIREsim
Der cFIREsim nutzt keine Monte-Carlo-Simulation3, sondern historische US-Renditen von 1871 bis 2015 (vermutlich die Daten von Robert Shiller).
Im Gegensatz zum Vanguard Calculator ist er nicht so intuitiv zu bedienen, bietet dafür aber auch sehr viel mehr Einstellmöglichkeiten. Ein echter Klassiker in der FIRE-Community!
Mit dem Laden des Videos akzeptieren Sie die Datenschutzerklärung von YouTube.
Mehr erfahren
Auch im nächsten der Teil der Serie werden wir den cFIREsim noch einmal wiedersehen. Dann schauen wir uns nämlich dynamische Entnahmen und verschiedene flexible Entnahmestrategien an.
1 Pfau, Wade: How Much Can I Spend in Retirement?: A Guide to Investment-Based Retirement Income Strategies, S. 76.
2 Für die Mathematisch interessierten: Es gibt wohl Verteilungen, die noch besser passen als das Modell von Black und Scholes.
3 Es existiert auch noch eine ältere Version des Rechners, in der man Monte-Carlo-Simulationen (auf Basis einer statistischen Verteilung) nutzen kann.
Hallo Oliver,
erstmal vielen Dank für deine fantastische Arbeit. Da hängt ziemlich viel Zeit dran und dafür ein dickes Lob. Ich muss das alles erst einmal verarbeiten 🙂
Viele Grüße
Alexander
Vielen Dank, Alexander! 🙂
Lass dir Zeit. 😉
Moin Oliver,
puh… durchaus interessant aber irgendwann wird es mir dann doch zu kompliziert und abstrakt 😉
Egal mit welcher Methode: Die Zukunft ist nicht vorhersehbar. Ich bleibe da mal flexibel aufgestellt. Irgendwelche Wahrscheinlichkeiten sind ein netter Anhaltspunkt aber irgendwie doch zu ungewiss!
Die Tools sind aber natürlich trotzdem interessant. Für das cFIREsim muss ich mir mal ein bisschen Zeit nehmen.
Danke für die Arbeit und die Links.
Beste Grüße
Vincent
Hallo Oliver,
Du steckst eine Wahnsinnssarbeit in die Recherche. Denn so einfach lassen sich die Infos nicht finden.
Und die Aufbereitung und verständliche Darstellung ist wirklich großartig.
Auch von mir ein dickes Lob! Herzlichen Dank.
Ergänzung: bei der Cfire Simulation ist nicht nur das Risiko auf geführt, dass man am Ende ins Minus läuft – also den Worst Case, sondern auch wie hoch das Vermögen (zum Vererben) bei den besseren möglichen Verläufen aussieht. Wenn man also mit einer 5% Wahrscheinlichkeit am Ende seine Wohnung in den letzten Jahren nicht mehr zahlen kann, könnte man mit einer wesentlich größeren Wahrscheinlickkeit auch mit einen sehr großen Vermögen abschließen. Das ist dann ja ganz beruhigend.
Wer nicht auf die geplante konstante Entnahmerate angewiesen ist und davon auch mal 4 Jahre nach unten abweichen kann, der erhöht die Wahrscheinlichkeit auf ein großes Vermögen und eine geringe Ausfallwahrscheinlichkeit.
Vielen Dank, Karl!
Genau so ist es.
Danke, Oliver.
Gibt’s bei dir jetzt pers. Strategieaenderungen nach den Simulations-Erkenntnissen bezueglich Kapitalbedarf, Entnahmeplan, Assetallokation, Sonst-was-Plan? LG Joerg
Hi Joerg,
die vorgestellten Tools kenne ich schon länger, ich hatte bisher nur noch keinen Blogartikel darüber geschrieben.
Einen konkreten Entnahmeplan habe ich auch noch gar nicht, da die Entnahmephase für mich ja noch ~10 Jahre in der Zukunft liegt. Wie dann meine Lebenssituation, mein Kapitalbedarf und ggf. weitere Einnahmequellen (und natürlich die Aktienmärkte) aussehen, kann ich heute noch nicht wissen. Darum mache ich einen genauen Plan erst dann, wenn es soweit ist. Bis dahin spare und investiere ich erstmal weiter drauflos. 🙂
Oliver, wie siehst du FIRECalc im Vergleich zu cFIREsim ?
FIRECalc finde ich auch nicht schlecht, aber cFIREsim gefällt mir ein Stück besser.
Die Funktionen von FIRECalc kennt cFIREsim im Wesentlichen auch, aber cFIREsim hat darüber hinaus noch ein paar mehr Einstellmöglichkeiten beim „Spending Plan“ und die Auswertung ist etwas umfangreicher.
Noch etwas: mich wuerde Deine Sicht als Erwiderung zu: https://www.gerd-kommer-invest.de/finanzielle-freiheit-fragezeichen/ interessieren?
(meine Sicht: im Prinzip hat er recht … aber die Konnotation koennte mehr ein „Nicht-sparen/investieren ist auch keine Loesung“ sein?)
Für Gerd Kommer ist Investieren anscheinend ein reiner Selbstzweck. Klar, damit verdient er ja seine Brötchen, und verkehrt anscheinend in Kreisen, in denen man materiell auf dicke Hose machen muss (schließlich behauptet er, Sparsamkeit würde den Freundeskreis verkleinern). Da sind ihm Leute, die Investieren mit einem bestimmten Ziel betreiben, wohl irgendwie suspekt. Den aggressiven Unterton („wer finanzielle Freiheit verfolgt ist doof“) finde ich ehrlich gesagt ziemlich nervig.
Auch wenn Gerd Kommer ein sehr intelligenter Mensch ist, er scheint Mr Money Mustache nicht wirklich gelesen zu haben. Ich interpretiere MMMs Ratschläge so: Führe ein tolles Mittelklasse-Leben, bezahle aber nur 25-50% der Kosten, die ein Otto Normal Verbraucher dafür ausgeben würde. Es geht überhaupt nicht um Einschränkung oder Geiz. Es geht darum, zu erkennen, was wirklich glücklich im Leben macht und wie man dies so kostengünstig wie möglich erreichen kann.
Und wirklich lächerlich finde ich den Teil mit dem Freundeskreis… Der Freundeskreis verkleinert sich vielleicht kurzzeitig, weil man seine verschwenderischen/ignoranten/veränderungsunwilligen „Freunde“ verliert. Normalerweise lernt man aber stets neue Leute kennen, vielleicht sogar welche, deren Lebensentwürfe mehr mit dem eigenen überein stimmen.
Viele Grüße
Benjamin
Hi Joerg,
es wird von mir an anderer Stelle noch eine Antwort zu Herrn Kommers Vortrag und seinem Blogartikel geben – dauert aber noch ein bisschen 🙂
Grundsätzlich kann ich mich Benjamin anschließen.
Und auch die umfangreiche Analyse von Mr. Happy im Forum fand ich treffend:
https://frugalisten.de/forum/topic/herr-kommer-belaecht-frugalisten/?part=3#postid-657
Hallo Oliver,
ich mag deinen wissenschaftlichen Ansatz und diese Beitragsreihe zu Entnahmestrategien.
Insgesamt beschäftigen sich viele Blogs (auch meiner) mit Vermögensaufbau und passivem Einkommen, aber man liest nur wenige Artikel über Entnahmestrategien. Am bekanntesten ist da noch die 4%-Regel. Vielleicht liegt es daran, dass man sich oft noch gar keine Gedanken macht, wie man das später macht. Viele sind ja gerade erst dabei die finanzielle Unabhängigkeit zu erreichen.
Freue mich auf den nächsten Teil!
Hi Oliver,
ausgezeichnete Arbeit!
Deine Artikel bieten sehr viel Lernstoff. Ich lerne hier gerne dazu. Allerdings bemerke ich bei mir eine gewisse Müdigkeit/Unbehagen ob dieser Thematik.
Auch auf die Gefahr hin, einen auf den Deckel zu bekommen: Ich bin froh, dass ich später nicht „entnehmen“, sprich Anteile verkaufen werde (und dabei Gefahr laufe, bei Null zu landen, wenn ich mich nicht ausführlich mit den wissenschaftlichen Erkenntnissen auseinander setze), sondern mich einfach auf die Dividendeneinnahmen meiner Aktien beschränke. Der Seeelenfrieden ist es mir wert.
Für ETF-Anleger allerdings ein wichtiges Unterfangen, welches du ausführlich erörterst. Klasse!
@Free
Warum hast Du denn immer Angst eines auf den Deckel zu kriegen???
Solange die Div-Rendite (Ausschüttung, Entnahme oder was man für ein Begrifflichkeitsmikado dafür spielen will…) auch 4 % beträgt ist es schnurz ob 70 Div-Aktien oder etf-Portfolio.
Die eine Fraktion behauptet die Ausschüttung sei stabiler und unzerstörbar und die andere beruft sich auf die bessere Asset Allocation bzw. die unbestechliche Mathematik.
Rein mathematisch treffen auch die Entnahmestrategien und deren Überlebenswahrscheinlichkeiten für die Freunde der Ausschüttung zu!
Weder ein Div-Aktien noch ein Etf-Portfolio entkoppelt sich von Wahrscheinlichkeitsbetrachtungen.
Alles andere ist Wunschdenken oder die irrationale Verherrlichung der eigenen Strategie.
Die Zukunft bleibt trotz aller Wahrscheinlichkeitsbetrachtungen ungewiss. Es geht nur darum zu betrachten, ob es vernünftig ist… dieses oder jenes Ergebnis zu erwarten.
@ sparta
Bei der Entnahmestrategie muss ich mir fundierte Gedanken darüber machen, wie ich konket entnehme.
Bei der Dividendenstrategie – die ich im übrigen gar nicht in Gänze verfolge – nicht. Nur auf diesen Unterschied wollte ich hinaus.
Ich habe einfach keine Lust, mir über den Verzehr meines Vermögens Gedanken zu machen. Ich peile auch keinen „Abschluss“ zum Lebensabend an (wie lange soll das Geld reichen?). Die Aktien werden wohl vererbt.
Hierbei verfolgt ja auch jeder seine eigene Lebensstrategie. Ich persönlich will gar nicht komplett aussteigen und nur vom Vermögen leben. Das „Können“ halte ich allerdings für eine attraktive Perspektive.
„Rein mathematisch treffen auch die Entnahmestrategien und deren Überlebenswahrscheinlichkeiten für die Freunde der Ausschüttung zu!“
Vielleicht mathematisch-theoretisch. In der Praxis wohl kaum. Schon mal von einem (weise ausgewählten und gut diversifizierten) Aktienportfolio gehört, das sich über die Dividendenausschüttungen selbst zunichte gemacht hat?
Ansonsten respektiere ich jede Strategie die Hand und Fuß hat. Da sind wir d áccord. Lassen wir doch die unsägliche Debatte zwischen Aktien und ETF einfach sein…. 😉 .
@Free
Den Wunsch sich keine Gedanken mehr machen zu müssen…
Ob ein Div – Portfolio wo sich die monatlichen Geldeingänge von der Willkür und der Geschäftsentwicklung grosser Konzerne abhängen, dies leisten kann?
Gedanken muss man sich immer machen, ausser man ist des Lebens müde.
Ich sehe es auch nicht als eine der unzähligen etf vs. Aktien Diskussionen an, sondern als Diskussion um Entnahmestrategien.
Angenommen Div-Strategien sind stabiler weil sie einer dynamischen Entnahmestrategie gleichen, bedeutet dies bei zu knapper Kalkulation für den Lebensunterhalt Einschränkungen…
Sich keine Gedanken machen zu müssen sieht für mich anders aus.
Ob ich von einem Ausfalldepot mit 2 % Div-Entnahme oder 2% Verkaufsstrategie gehört habe ist statistisch irrelevant.
Stabiler wie eine 4% Entnahme oder auch 4% Dividendenausschüttung ist es definitiv.
Wenn man mal ganz verschiedene Simulationen durchspielt, dann kommt man am Ende irgendwo im Bereich einer 3 bis max 4% Regel raus bei der Betrachtung eines 40 Jahres Zeitraumes und 95% Überlebenswahrscheinlichkeit.
Da bei mir irgendwann in den nächsten 3 bis 10 Jahren die Entnahmephase beginnt und wir uns vielleicht ehrer im oberen Bereich der Entwicklung der Aktienmärkte stehen werde ich in dieser Phase mit einem etwas höheren risikoarmen Portfolio starten (30 % Risikoarm) und dort mit der Entnahme starten.
Aktuell ist der Zeitpunkt für den Beginn einer Entnahme wahrscheinlich risikoreicher als vor 8 Jahren. Da sollte man etwas vorsichtiger rangehen.
Hallo Karl,
sind die von Dir angegebenen 3% bis max. 4% vor oder nach Steuern? Ansonsten bleiben ca. 2,3% bis 3% übrig.
Sagen wir mal so. Das sind alles Modellrechnungen ob nun historisch, historisch Monte Carlo o.ä. und damit gibt keine eine Gewissheit, dass es tatsächlich aufgeht.
Aber wenn man mal alles so durchspielt dann müßten (!!) 3% mit Inflationsausgleich und nach Steuern hinkommen. Bei den 95% Überlebenswahrscheinlichkeit ist die Wahrscheinlichkeit relativ kurz vor Ende ohne Geld darzustehen eben bei 5%. In 95 Prozent bleibt was übrig. Was da übrig bleibt kann ein auch ein Vielfaches davon sein, was einmal eingesetzt wurde. Aber sicher ist nichts. Berechnungen hin und her.
Wichtig ist sicher das Rebalancing in der Entnahmephase und ein ausreichend großer Risikopuffer in risikoarmen Anlagen. Dies gilt umso mehr, wenn die Entnahmephase in eine bereits sehr langen anhaltenden Aufschwungphase am Aktienmarkt beginn.
Am Ende bleibt: Vielleicht läuft es in den nächsten 30 oder 40 Jahren auch ganz anders als in den letzten 30 oder 40 Jahren.
Das ist ein Denkfehler. Du musst nur den Gewinnanteil der jährlichen Entnahme versteuern.
Karls Statement passt genau zu meiner Situation. Ich bin in der Entnahmephase 😉
Vielen Dank für die hervorragende Ausarbeitung! Das spart mir einiges an eigener Recherche. Wo finde ich denn den Monte Carlo Simulator, der die aktuelle Niedrigzinsphase in der Anfangsphase stärker gewichtet inklusive serieller Korrelationen?
Das Modell der Altersteilzeit wird mir immer sympatischer. Hier gehe ich in Teilzeit, wenn mein Vermögen dies zulässt. Dies könnte beispielsweise mit der 4% Formel definiert werden). Bei diesem Ansatz bleibe ich krankenversichert, so dass ich für Kapitalerträge keine Krankenversicherung zahlen muss. Ich erfahre so mehrere Schritte zur Freiheit und dadurch immer wieder neue Erfolgserlebnisse. Ich kann jedes Jahr in Teilzeit das aktuelle Vermögen neu mit der Simulation bewerten. Da die Laufzeit sich jedes Jahr verringert wird die Wahrscheinlichkeit des Überlebens meines Vermögens sich zu meinen Gunsten verändern. Vor allem, wenn das Vermögen in der Zwischenzeit weiter wächst.
hallo Oliver,
vielen Dank für Teil 4, die Rechner sind toll, (den Artikel muss ich aber genauer studieren und auch mehrfach lesen) ich habe schon ein wenig herumgespielt damit, Rente, Dividende und Mieteinnahmen reichen in meinem Fall aus, ich bin aber schon 60 und das hat mit FIRE natürlich nicht so viel zu tun,
Alles berechnen lässt sich nicht, ich werde die Entnahme in den ersten 3 Jahren sowieso eher sehr konservativ planen, fällt mir auch nicht schwer da ich nicht vorhabe, im Rentenalter plötzlich konsumieren zu wollen als gäbe es kein Morgen mehr.
Liebe Grüsse!
Danke Oliver!
Wie immer sehr spannend und informativ geschrieben. Für mich gehören die Entnahmestratetien momentan zu den spannendsten Themen. Bin froh, dass ich auf deinen Blog gestossen bin.
Spannend geschrieben. Hast du mal überlegt, auch ein paar Blog-Einträge zum Thema Software-Entwicklung zu schreiben? Wäre spannend.
Hallo Oliver,
tolle Artikelserie!
Wie ist deine Meinung zu den Rechnern von portfoliocharts?
https://portfoliocharts.com/calculators
Die Daten gehen hier auch auf internationale Assets zurück und sind nicht so US lastig.
Würde mich über ein Review freuen 🙂
Beste Grüße
Christoph
Hallo, Danke für die ganzen Infos!
Einen Aspekt konnte ich bisher leider weder hier noch in anderen Blogs zum Thema FiRe finden: Die Berücksichtigung von Steuern und Sozialabgaben in Deutschland.
Unter welchen Umständen muss man die ca. 14-15% Abgaben für die GKV zahlen? Was für einen Einfluss haben die Einkommenssteuer (bzw. bei hinreichend hohen Einkünften nur die Abgeltungssteuer) und der Solidaritätszuschlag? Wenn man davon ausgeht, dass es Jahre mit Verlusten (keine Steuer, aber ein Mindestbeitrag für die GKV?) und Jahre mit Gewinnen (Steuern bzw. „Verbrauch“ von Verlustvortrag plus Beitrag für GKV) gibt, sollte das einen deutlichen Einfluss auf die Resultate haben.
Falls es hierzu schon Veröffentlichungen oder sogar „Rechner“ gibt, wäre ich Ihnen sehr denkbar, wenn Sie hierzu die Quellen schreiben könnten.
Freundliche Grüße
Jürgen
Hallo Jürgen,
zum Thema Steuern und GKV wird es in der Serie noch einen eigenen Artikel geben, kann aber noch ein paar Monate dauern.
Steuern zahlt man grundsätzlich nicht unbedingt abhängig davon, ob es in einem Jahr Gewinne oder Verluste gab. Mit Ausnahme der Vorabpauschale auf ETF-Kursgewinne zahlt man Steuern auf Kursgewinne erst beim Verkauf. Die absoluten Entnahmebeträge sind für die Versteuerung also relevanter als die Kursschwankungen des Depots.
Verluste können bei der Vorabbesteuerung auch nicht jährlich gegengerechnet werden, sondern ebenfalls erst beim Verkauf der Anteile, vgl. hier:
https://zendepot.de/etf-fonds-steuern/#comment-10855
Hier als Ergaenzung ein sehr schoener Artikel von Weis & Kommer zu Hilfsmitteln, um noetige Sparrate, moegliche Entnahmerate und Auswirkung der SoRR(Seq.ofReturnRisks) abzuschaetzen (MonteCarloSimulation, MCS):
https://www.gerd-kommer-invest.de/monte-carlo-simulation-als-prognoseverfahren
Die Verwendung historischer Renditereihenfolgen (im Bootstrapping oder besser) in deren historischen Abfolge werden kurz erwaehnt, lineare Schoenrechnerreien anderer „Finanzexperten“ (zB 5% Realrendite p.a. jedes Jahr) zurecht als Sandkastenspielerei angesprochen.
Exzerpt:
Die gezeigte Simulation mit den gutbetuchten Meiers (1Mio mit 50, 10 a weitere 50k/a ansparen, 1,5Mio mit 60, 50k Entnahme p.a. ab 61) betrifft wohl nur wenige Leser hier, zeigt aber exemplarisch die Schwankungsbeite moeglicher Entwicklungen bis zum Alter von 90 (18% Failure-Rate bis 90!).
MCS „uebertreibt“ bei der Failure-Rate, da unberuecksichtigt bleibt, dass der Markt ein Gedaechtnis hat (nach Crashs folgen eben KEINE zufaelligen Kurse sondern es geht erstmal laenger wieder hoch – ohne weitere Nackenschlaege/“zufaellige“ neue Tiefs – vergl. gedehntes Gummiband-Analogie bzw Regression zum Mittelwert-Verhalten). Siehe dazu auch Links zu earlyretirementnow.com weiter oben.
Die 4% „Daumen-Regel“ wird als zuu optimistisch eingeschaetzt (allerdings ist im Artikel auch „nur“ ein 50/50 Portoflio Renten/Aktien Grundlage mit 2,9% p.a. Realrendite).
Viele setzten ja deshalb auf 3,3-3,5% Entnahme bei 80-90% Aktien-ETF-Anteil (und nicht 4%).
Eine hoehere Aktien-Quote koennte/wuerde laut MCS zu hoeheren Spannbreiten fuehren (v.a. Failure).
Fuer mich ist wichtig: Es gibt keine (absolute) Sicherheit!
Da Maerkte reflexiv wirken und sich entwickeln, ist auch unklar ob sehr lange Zeitreihen (500 Jahre) helfen wuerden „mehr Sicherheit“ in die Berechnungen zu bekommen (die Maerkte waren schon vor 100 Jahren voellig anders als heute, oder? Wer weiss was in 20-30 Jahren ist)
Ich weiss, dass ich nix weiss!?
Ueberlege selbst, wo wir in 10, 20, 30 Jahren sein koennten? Was ist wahrscheinlich fuer Zinsentwicklung? Immobilien? Bevoelkerungswachstum/Migration? Welche Regionen, Firmen werden sich viell. wie entwickeln?
Wir pers. begegnen Unsicherheit mit ~ Drittelmix: gesetzl.Rente / AktienETF-Depot / mietfr. Wohnen
Ausserdem sind und bleiben wir in Gottes Hand ;-). Lebe jetzt!
weil’s dazu gut passt hier Karstens neuster Post:
https://earlyretirementnow.com/2018/11/05/retired-at-the-market-peak-still-not-worried/
zu:
– Wann die 4%-Regel gut klappt (nicht am Market-Peak, aber sonst ganz OK)
– zu Makro-Update: kommt der Crash jetzt oder spaeter? (spaeter! Inverse-Zinskurve? – noch nicht; PMI? – noch bombig; Arbeitslosigkeit? – noch gering)
– was macht der Shiller CAPE: sollte sinken (Niedrig-Gewinn-Jahre 2008/2009 schleichen sich demnaechst aus)
Hi,
erstmal großes Lob zu deiner Seite. So eine gute Zusammenfassung habe ich noch nirgendwo gesehen.
Ich habe zwei Punkte die ich ansprechen möchte.
1. Die Summe der Würfe ist >1200, was bei 1200 Würfen doch recht merkwürdig erscheint.
2. Was ist mit Anlagen die keine Anleihen sind und trotzdem eine negative Korrelation besitzen(Gold). Da gibt es ja auch ETF’s. Wenn man noch ein paar ausmachen kann und diese mit ins Portfolio nimmt kann man ähnlich wie mit den Anleihen das Risiko ggf. auch noch minimieren. Da gibt es bestimmt auch noch interessante Parameter die man beachten muss(z.B. Zusammensetzung).
Gruß und weiter so.
Hallo Marco,
Es wurde ja nirgendwo behauptet, dass die Anzahl der Würfe exakt 1200 beträgt.
In der Bildunterschrift steht „ca. 1.200“, also ungefähr 1.200 Würfe.
Negativ zueinander korrellierte Assetklassen sind prinzipiell immer gut für die Diversifikation eines Portfolios.
Wie groß allerdings der „optimale“ Portfolioanteil einer zusätzlichen Assetklasse ist (bezogen auf das Verhältnis aus Rendite und Volatilität), das steht dann nochmal auf einem anderen Blatt.
Mit den Mitteln der modernen Portfoliotheorie nach Markowitz kann man für jedes Portfolio eine „Effizienzlinie“ berechnen und damit die optimale Portfolioallokation (jedenfalls für die Vergangenheit) bestimmen. Was dabei herauskommt, hängt oft von den gewählten Daten und Zeiträumen ab.
Diese Studie hier kommt etwa zu dem Ergebnis, dass ein Portfolio, das zu 60 % aus Aktien und 40 % aus Anleihen besteht, durch eine Beimischung von 20 % Gold am meisten profitiert:
http://proactiveadvisormagazine.com/what-is-the-optimal-portfolio-allocation-to-gold/
Ich würde mir aber wie gesagt immer ganz genau ansehen, wer solche Studien herausgibt, welche Daten und Parameter gewählt wurden. In vielen Studien, die ich im Internet zu dem Thema gefunden habe, werden etwa Renditedaten von 1972 bis heute verwendet. 1972 stand der Goldpreis auf dem historischen Tiefstand, heutee steht er nahe dem historischen Maximum. Dadurch ist die Rendite von Gold in diesem Zeitraum deutlich höher als im langfristigen historischen Schnitt, was die Berechnungen zugunsten dieser Assetklasse verzerrt.
Hi Oliver
Grundsätzlich ein guter Artikel. Als Ökonom möchte ich dich gerne darauf hinweisen, dass für die Renditen für gewöhnlich keine Log-Normalverteilung zur Anwendungkommt. Eine gängige Annahme sind „Normalverteilte Renditen“ was dann zu „Log-Normalverteilten Preisen“ führt. Ist ein technisches Detail, wäre aber schade, da der Artikel sonst gut ist.
Gruss
Hallo Yoda,
danke für die Richtigstellung! 🙂 Da lag ich tatsächlich falsch – die Aktienkurse sind also lognormalverteilt, hingegen die Renditen daraus folgend normalverteilt.
Ich habe die entsprechenden Textstellen im Artikel korrigiert.
Hallo Oliver,
vielen Dank für diese Artikelserie und auch die anderen Beiträge auf deiner Webseite!
Im Artikel 2 der Entnahmestrategie Serie erwähnst du, dass das sequence-of-returns Risiko natürlich auch auf das Endergebnis eines Sparplans Einfluss hat. Daher würde ich gerne mit den vorgestellten Simulationen mögliche Ergebnisse eines Sparplans berechnen lassen. Gehe ich richtig vor wenn ich dazu in cFIREsim die Entnahme Rate auf Null setze, die Dauer des „Entnahmezeitraums“ auf z.B. 25 Jahre einstelle und zusätzlich mittels eine Pension meine jährliche Sparrate abbilde? Oder mache ich da einen Denkfehler?
Danke und Gruß,
Klaus
Hallo Klaus,
ich denke, das könnte so funktionieren.
Hallo Oliver,
danke erstmal für diese informative Serie. Ein Mini-Hinweis: in diesen Artikel fehlt der Link auf den nächsten Teil der Serie.
Viele Grüße
Jenni
Hallo Jenni,
sehr aufmerksam, vielen Dank! Ist jetzt eingefügt. 😉
Hallo Oliver, tolle und sehr informative Artikelserie, danke dafür.
Ein Fehler ist mir jedoch aufgefallen: Aktienkurse sind nicht normalverteilt. Wenn dem so wäre, wären Kurseinbrüche wie 2008 oder 2020 nur alle paar Milliarden Jahre der Fall. In der Realität sind sie jedoch deutlich häufiger (Der 2008er Crash war ein 20 Sigma-Ereignis)
Das Black-Scholes-Merton Modell hat auch so prima funktioniert, das der von diesen Leuten betriebene Fond pleite gegangen ist und fast das Finanzsystem mit sich gerissen hätte (LTCM, 1998)
Man kann (und sollte) in ETFs investieren, sollte aber theoretisieren über die Kursentwicklung in Jahren und Jahrzehnten unterlassen. Es ist nicht vorhersehbar. Grundsätzlich nicht, mit keinem Modell.
Deinen „Wann kann ich in Rente gehen-Rechner“ nehme ich jeden Monat, bin mir aber immer im klaren, das das nur EIN mögliches Ergebnis ist. Und das Szenarien wie jahrzehntelange Seitwärtsbewegungen (wie zb. nach 1929) eine sehr reale Bedrohung sind.
Hallo Matthias,
hast du für die Falsifizierung des Black-Scholes-Modell eine seriöse Quelle?
Es behauptet übrigens niemand, dass Aktienrenditen ganz genau normalverteilt sind. Im Artikel schreibe ich ungefähr normalverteilt. Gemeint ist: Eine Normalverteilung beschreibt die Renditeverteilung für viele Modelle und Simulationen hinreichend genau.
Für die meisten Entnahmesimulationen liefern historische Daten und eine einfache Normalverteilung recht ähnliche Ergebnisse, was für die Normalverteilung als Modell spricht.
Dass Kurseinbrüche wie 2008 ein „20-Sigma-Ereignis“ mit einer Wahrscheinlichkeit in der Größenordnung von 1:10^9 sein sollen, kann ich partout nicht nachvollziehen.
2008 betrug die Rendite des MSCI World -38 % (inkl. reinvestierten Dividenden – http://www.clever-und-erfolgreich.de/etf-rendite/).
Bei 6 % Durchschnittsrendite und einer Standardabweichung von 20 % beträgt die Wahrscheinlichkeit für eine Rendite von -38 % oder weniger ca. 1,4 % (das kann man z.B. hier nachrechnen: http://onlinestatbook.com/2/calculators/normal_dist.html). Das sind nicht 20 Sigma, sondern 2-3 Sigma, und auch kein Ereignis, das statistisch alle paar Milliarden Jahre, sondern alle 71 Jahre stattfindet – acht Größenordnungen von deine Behauptung entfernt.
Wie kommst du da auf 1:10^9 und 20 Sigma?
Das Black-Scholes-Modell ist eigentlich zur Optionspreisfindung gedacht. Bestandteil davon ist, das man die Schwankungen des zugrunde liegenden Wertpapiers zu berechnen versucht.
Das Black-Scholes Modell macht zwei vereinfachende Annahmen:
-Die Standardabweichung des Wertpapiers sei gleichbleibend. Das ist in der Realität aber nicht der Fall. (das die Standardabweichung sich ändert, gerade in Abschwungphasen, schreibt z.b. Kommer, Souverän investieren, Seite 89, neueste Ausgabe, aber auch mein Morningstar-Link unten)
-Die Verteilung der Kurse sei Gaussch.
Das ist auch nicht der Fall.
Das hat Mandelbrot schon in den 60ern gezeigt, auch Taleb und andere. Die Nachweise sind alle mathematisch recht anspruchsvoll. Ich habe Links eingefügt, besser ist aber das Buch von Taleb.
Taleb zeigt im „Schwarzen Schwan“ (2007) sehr verständlich, warum die Gaussche Glockenkurve in weiten Bereichen nicht anwendbar ist (und das Black-Scholes-Modell, das sie verwendet)
Das gefährliche ist, das sie „fast“ richtig erscheint. Komplett falsch ist sie aber bei seltenen Ereignissen, und das sind die Gefährlichen.
https://web.williams.edu/Mathematics/sjmiller/public_html/341Fa09/econ/Mandelbroit_VariationCertainSpeculativePrices.pdf
http://optionsoffice.ru/wp-content/uploads/2013/08/Nassim-Taleb_Why-we-have-never-used-the-BSM-option-pricing-formula.pdf
Zum 20-Sigma-Event: Die Auswirkungen der Krise 2008 waren nicht in allen Bereichen gleich. Den MSCI World auf Jahressicht hat es weniger getroffen als beispielsweise den LIBOR-Zinssatz oder einzelne Märkte. Auch ist in dem Fall die Tages-oder Monatsbetrachtung wichtiger. Ich habe hier auf ein Dokument der JP Morgan verlinkt. Die sehen da ein 18 Sigma-Event.
Seite 27 schildert das Problem ganz gut.
https://www.jpmorgan.com/jpmpdf/1320675765434.pdf
Goldman Sachs (David Vinair) sprach 2007 beim Zusammenbruch zweier Fonds von „mehreren 25-Sigma-Events hintereinander“ (das die Wahrscheinlichkeit größer ist, das sein Modell falsch ist, hat er wohl nicht in Betracht gezogen…)
Wie ich oben schrieb, ist die Standardabweichung veränderlich. Je nach den verwendeten Daten kommen dann sehr unterschiedliche Ergebnisse heraus.
Und natürlich muß man die Daten VOR dem Ereignis nehmen, nicht hinterher.
Hier ein Morningstar-Link (kostenlose Registrierung erforderlich)
https://www.morningstar.de/de/news/141557/warum-risikobetrachtungen-in-der-praxis-oft-zu-kurz-greifen.aspx
Die 5-Jahres-Standardabweichung war 2007 niedriger als 14, eher Richtung zehn. Die 12-Monats-Standardabweichung war in den Jahren vor 2007 um die 11. Das wären wohl die Zahlen, die ein Anleger damals als Referenz genommen hätte. Mit Deinem Rechner (danke übrigens) komme ich mit einer Standardabweichung von 14 auf 1:1250. Mit Standardabweichung von 11 will der Rechner nicht mehr arbeiten, ich komme da auf 4 Sigma, also ca 1 Event in 15000 Jahren.
Man sieht: nur durch unterschiedliche „ Messung“ der Standardabweichung kommt man hier auf Ergebnisse zwischen 1:71 und 1:15.000.
Das die Gaußkurve da nicht weiterhilft, zeigt auch dein eigener Morningstar-Link ganz gut. (Seite 9: Die Zahl der 3-Sigma Events ist 10 höher als sie sein sollte)
In wie weit betrifft das jetzt einen Anleger, der langfristig jahrzehntelang in ETFs investiert? Wenig. Die Monte-Carlo-Simulationen zeigen ja sehr gut, wie sehr die Entwicklung eines Portfolio von völlig unbekannten Entwicklungen beeinflusst wird. Und das sind nur die „Known unknowns“. Die „unknown unknowns“, also das unbekannte Unbekannte, taucht da überhaupt nicht auf.
Man sollte äußerst vorsichtig sein, wenn jemand versucht, Risiko zu „messen“. Ein globalisiertes Portfolio kann Risiko minimieren, man kann über mehrer Anlageklassen diversifizieren, aber „messen“ lässt sich das Risiko daraus nicht wirklich. Alle Werkzeuge wie VaR, Standardabweichung, maximum Drawdown etc, sind immer nur ein Blick in die Vergangenheit, und es lassen sich keinerlei Schlüsse für die Zukunft ziehen.
Hallo Matthias,
vielen Dank für deine sehr ausführliche und gut belegte Antwort! Dem habe ich nichts mehr entgegenzusetzen/hinzuzufügen.
Meine Werte für Durchschnittsrendite (6 %) und Standardabweichung (20 %) hatte ich diesem Artikel von Gerd Kommer entnommen, sie bezogen sich auf den MSCI ACWI IMI zwischen 2002 und 2017:
https://www.gerd-kommer-invest.de/fragwuerdigkeit-von-einzelaktieninvestments/
Nach langer Zeit noch ein Kommentar. Die Berechnung des Risikos ist, wie oben ja noch mal gezeigt schwierig. Die praktische Fragestellung ist ja, was soll man tun, wenn man in der Entnahmephase in eine Crash gerät. Insbesondere, wenn der Crash in den ersten Jahren stattfindet oder vielleicht auch zweimal.
Auszahlungen massiv nach unten korrigieren wäre eine Maßnahme.
Eine andere, bisher noch nicht debatierte ist : Kredite aufnehmen und dann in Höhe des Kredites für 1 bis 3 Jahre nichts entnehmen. Wichtig ist dann natürlich eine sinnvolle Tilgungsregelung . Ein Aktiendepot könnte man so theoretisch bis 50% beleihen. In der verschärften Variante könnte man auch zusätzlich Kredite im Crash aufnehmen und in den fallenden/gefallene/steigenden Markt investieren. Da sollte man sich schon vorher um eine Kreditlinie kümmern, damit man auch schnell handeln kann. Diese im Crash auf Kredit investieren ist natürlich mit einem gewissen Risiko behaftet und ich würde es erst ab einem Minus von höchsten Erreichten Kurs von 30 bis 40% machen. Denn dann dürfte es theoretisch nicht mehr so weit bis zu einer Bodenbildung sein.
Die ganze Kreditidee beruht natürlich auf der Annahme, dass die Kurse nach einem Crash wieder stark steigen.
Wertpapierkredite sind eine prima Sache, sind ja im Prinzip ein Dispo-Kredit, der wesentlich billiger ist (bei meiner Depotbank 3,98% eff. Jahreszins). Kann man im Crash durchaus nehmen, jedenfalls in der Ansparphase. Mit der Höhe der Beleihungssumme muß man aber aufpassen: Wenn der Depotwert unter die beliehene Summe fällt, kann die Bank deine Anteile verkaufen wenn Du den gezogenen Kredit nicht sofort zurückzahlen kannst (bis das Depotwert/Kreditverhältnis wieder passt). Wäre natürlich doof, wenn die Bank dann bei -51% anfängt, dein Zeugs zu verkaufen…
Um einen simplen Crash auszusitzen, ist meiner Meinung nach ein gewisses Maß an Cash das sinnvollste. Auch deswegen, weil Banken Kredite nicht vergeben MÜSSEN und in Bankenkrisen evtl weder wollen, noch können. Bin mit nicht so sicher, ob ein Bankkredit in 2008 geklappt hätte.
Was bei all den Überlegungen aber immer fehlt, ist eine Lösung für das Problem, wenn Aktienkurse fallen, und sich eben NICHT schnell wieder erholen, sondern über einen längeren Zeitraum deutlich unter dem Niveau vom Zeitpunkt des „Rentenbeginns“ liegen. Was dann oft auch mit einer Arbeitsmarktkrise einhergehen dürfte, womit die Lösung, einfach ein paar Jahre zu arbeiten, wegfallen dürfte.
Eine Idee hätte ich allerdings auch: In einer Krise kann man durchaus Geld verdienen, indem man sie ausnutzt. Man macht sich selbstständig. Verdient Geld damit und tut noch was sinnvolles für die Gesellschaft. (Mal als Beispiel: man kauft sich ein E-Lastenrad und geht für alte Menschen einkaufen) Dafür braucht man 2 Dinge: Startkapital und Zeit, beides haben Frugalisten im Überfluss.
Oliver Du schreibst:
„Dafür habe ich heute zwei Videos mitgebracht, in denen ich euch zwei dieser Rechner einmal genauer vorstelle: den Vanguard Nestegg Calculator und den cFIREsim.“
Ich habe die Videos nirgends gefunden?
Hallo Frank,
die Videos sind eigentlich im Artikel oben eingebettet.
Ansonsten findest du sie aber auch hier:
https://www.youtube.com/channel/UCzokmBcSgYh5NcGVQpdlpbw/videos